
Normal & Shear Stress Chapter 1 - [PDF Document] Stresses on Inclined Sections Shear stress and shear strain. Equality of shear stresses on perpendicular planes. Hooke’s law in shear. Normal and shear stresses on inclined sections. Maximum stresses on a bar in tension. Introduction to stress elements. 2 Shear stress Shear stress acts tangential to the surface of a material. Top view Side view Greek letter τ (tau) V = shear force A …
Lecture 5 handout HT08 University of Oxford
Normal stresses in shear flow TA Instruments. Calculation of normal and shear stress on a plane. Frequently it is necessary to calculate the normal and the shear stress on an arbitrary plane (with unit normal …, Tectonic shear stress on faults cannot in general be changed without also changing fault-normal stress (altering its frictional strength) and the level of mean stress ( σ ¯ = [σ 1 + σ 2 + σ 3]/3) (Sibson, 1991)..
PDF The conventional strain gauge slitting method is usually used to determine the residual stress component normal to the slit plane. Therefore, it is assumed that residual shear stresses Shear stress (Tau)= -Normal stress (Sigma)*cos(theta)*sin(theta) However, this is a special case to only the analysis of a beam using an inclined section, which doesn’t apply to normal sections or to sections under torsion.
16th Australasian Fluid Mechanics Conference Crown Plaza, Gold Coast, Australia 2-7 December 2007 Effect of tear additives on the shear stress and normal stress acting on the ocular surface The normal stress σ and shear stress τ acting on any plane inclined at θ to the plane on which σ y acts are shown in Fig. 7.1(b). The stresses σ and τ may be expressed in terms
• How do the normal and shear components of stress acting on a plane at a given point change as we change the orientation of the plane at the point. • How might stresses vary from one point to another throughout a contin maximum maximum shear stress and the maximum bending stress. 7.2 kN 3.7 m 3.7 m Solution : The beam is symmetrical about its mid-point, so the reactions are equal: R A = R B = 7.2 2 = 3.6 kN The load and reactions are concentrated forces so the shear forces are constant between the concentrated loads. For example, take any section through the beam at 0 < x < 3.7 m from the left end of the …
JOURNAL OF MATERIALS SCIENCE 11 (1976) 445-457 Pressure and normal stress shear yielding effects in J.C.M. LI, J. B.C. WU Department of Mechanical and Aerospace Sciences, and Materia/s Science Program, Stress is the resistance to an applied force.Mathematically, it is the internal restoring/resisting force per unit area over which the force is acting upon. Basically, there are 3 types of stress. 1. Normal stress-Tensile and Compressive. 2. She...
Normal Stress, Bending Stress, & Shear Stress Stresses in Beams In a separate article entitled “Structural Analysis of a Beam” there was a brief discussion of stresses and … normal and shear stress.pdf - Download as PDF File (.pdf), Text File (.txt) or read online.
Stresses on Inclined Sections Shear stress and shear strain. Equality of shear stresses on perpendicular planes. Hooke’s law in shear. Normal and shear stresses on inclined sections. Maximum stresses on a bar in tension. Introduction to stress elements. 2 Shear stress Shear stress acts tangential to the surface of a material. Top view Side view Greek letter τ (tau) V = shear force A … 11/05/2016 · I have a vibrating structure, and using eigenfrequency analysis to get the natural frequency. I want to evaluate the normal stress and shear stress along …
4 19 Example Problem 4-4: Combined Normal and Shear Stress • A center mounted chain drive system transmits 20 hp at a speed of 500 rpm. • If the sprocket has a pitch diameter of 8 inches, would this be an acceptable design if the Normal Stress, Bending Stress, & Shear Stress Stresses in Beams In a separate article entitled “Structural Analysis of a Beam” there was a brief discussion of stresses and …
dx M(x) M(x)+ dM(x) dx N.A. dx Fig. 3 Length of beam dx with normal stress distribution due to bending moment Summing the forces horizontally on this infinitesimal element, the stresses due to the bending The compression stress is perpendicular to (or normal to) the column section and is thus a "normal stress". Shear stress is parallel to the section plane. This is harder to describe, but an example of this is a screw holding up a small hook in your closet.
4AN007 lim lim ' g& →w = 0 N 1 2G (12) In Figure 5 the dynamic data are compared to the steady shear viscosity and normal stress. The correlation holds over a wide range of shear rate Shear stress (Tau)= -Normal stress (Sigma)*cos(theta)*sin(theta) However, this is a special case to only the analysis of a beam using an inclined section, which doesn’t apply to normal sections or to sections under torsion.
PDF Aim . Callus is a risk factor, leading to severe diabetic foot ulcer; thus, prevention of callus formation is important. However, normal stress (pressure) and shear stress associated with Stresses on Inclined Sections Shear stress and shear strain. Equality of shear stresses on perpendicular planes. Hooke’s law in shear. Normal and shear stresses on inclined sections. Maximum stresses on a bar in tension. Introduction to stress elements. 2 Shear stress Shear stress acts tangential to the surface of a material. Top view Side view Greek letter τ (tau) V = shear force A …
Stress MIT OpenCourseWare

Stress MIT OpenCourseWare. Stresses on Inclined Sections Shear stress and shear strain. Equality of shear stresses on perpendicular planes. Hooke’s law in shear. Normal and shear stresses on inclined sections. Maximum stresses on a bar in tension. Introduction to stress elements. 2 Shear stress Shear stress acts tangential to the surface of a material. Top view Side view Greek letter τ (tau) V = shear force A …, Explanation: In a body loaded under plane stress conditions, the number of independent stress components is 3 I.e. two normal components and one shear component. 5. If a bar of large length when held vertically and subjected to a load at its lower end, its won-weight produces additional stress..
What is the difference between stress and shear stress. During bending, in most cases a normal stress in tension and compression is created along with a transverse shear stress. The only time shear would not be a factor is if the beam is only under a moment. Transverse shear stress will be discussed separately., 11/05/2016 · I have a vibrating structure, and using eigenfrequency analysis to get the natural frequency. I want to evaluate the normal stress and shear stress along ….
Normal & Shear Stress Strength of Materials Questions

14.330 Shear Strength Faculty Server Contact. • The corresponding average shear stress is, • The resultant of the internal shear force distribution is defined as the shear of the section and is equal to the load P. • Corresponding internal forces act in the plane of section C and are called shearing forces. • Shear stress distribution varies from zero at the member surfaces to maximum values that may be much larger than the PDF The conventional strain gauge slitting method is usually used to determine the residual stress component normal to the slit plane. Therefore, it is assumed that residual shear stresses.
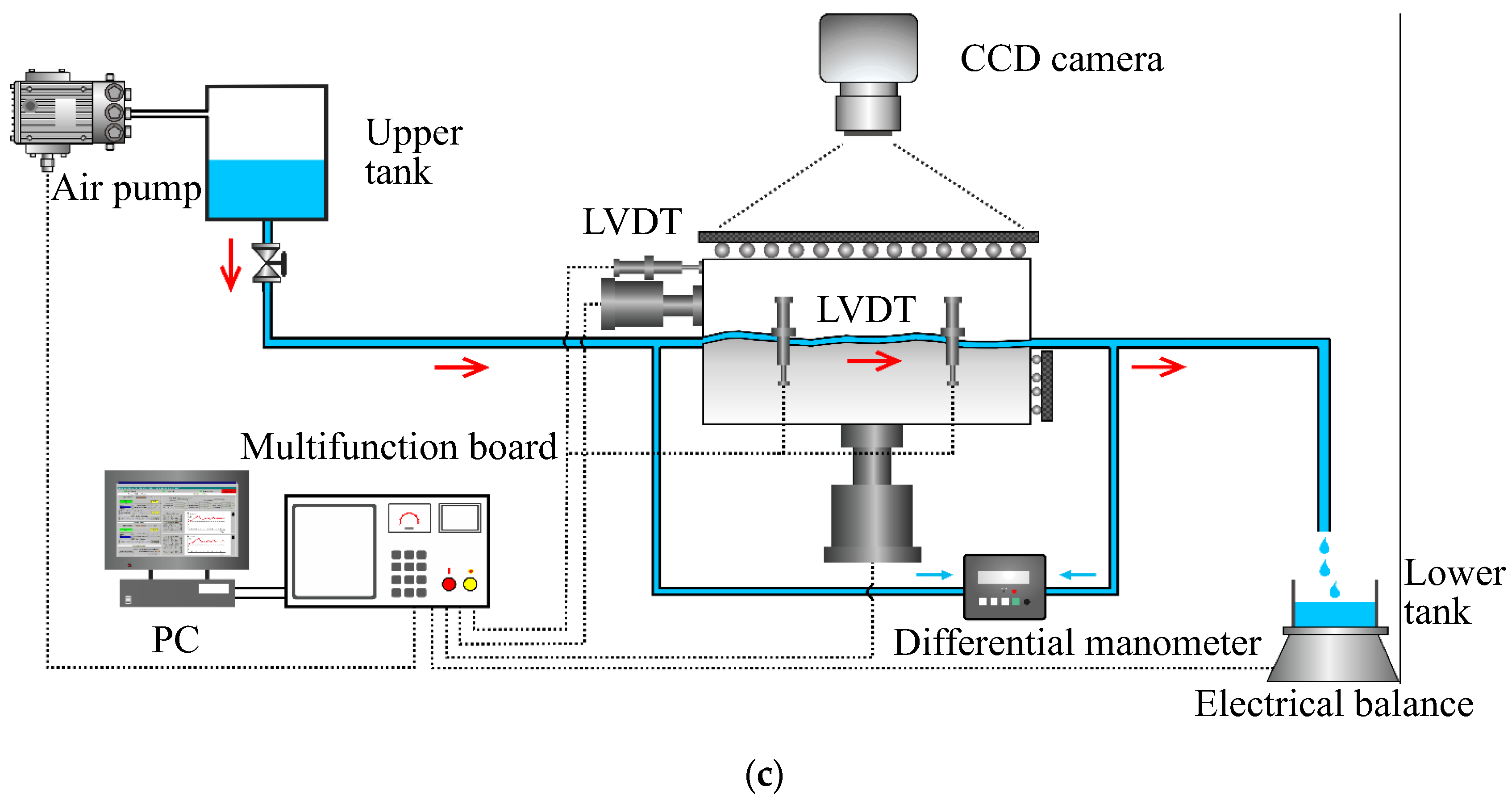
PDF Aim . Callus is a risk factor, leading to severe diabetic foot ulcer; thus, prevention of callus formation is important. However, normal stress (pressure) and shear stress associated with cases of pure normal stress and pure shear, it is true for more complicated conditions as well. Deformation due to shear stress: In pure shear (𝜎𝜎= 0), the size of the faces stay the same, but the object changes shape.
Normal stress & Shear Stress 1. Introduction • Mechanics of materials is a study of the relationship between the external loads on a body and the intensity of the internal loads within the body. Normal Bending Strain creates Normal Stress V H U H E y y is measured from the neutral axis ρ is the radius of the curvature of the beam The bending moment is all
maximum maximum shear stress and the maximum bending stress. 7.2 kN 3.7 m 3.7 m Solution : The beam is symmetrical about its mid-point, so the reactions are equal: R A = R B = 7.2 2 = 3.6 kN The load and reactions are concentrated forces so the shear forces are constant between the concentrated loads. For example, take any section through the beam at 0 < x < 3.7 m from the left end of the … • The corresponding average shear stress is, • The resultant of the internal shear force distribution is defined as the shear of the section and is equal to the load P. • Corresponding internal forces act in the plane of section C and are called shearing forces. • Shear stress distribution varies from zero at the member surfaces to maximum values that may be much larger than the
Thus, the plane of maximum shear stress is always ±45 from the plane of maximum normal stress. These corresponding two values of θ may then be substituted into (5.7) to obtain the maximum and minimum values of σ is referred as normal stress, another type of stress is called shear stress sign convention of the normal stresses are : tensile stress as positive and compressive stress as negative
The compression stress is perpendicular to (or normal to) the column section and is thus a "normal stress". Shear stress is parallel to the section plane. This is harder to describe, but an example of this is a screw holding up a small hook in your closet. but the normal stress "x calculated from the flexure formula are not significantly altered by the presence of shear force and warping we may justifiably use the theory of pure bending for calculating " x
Normal Stress, Bending Stress, & Shear Stress Stresses in Beams In a separate article entitled “Structural Analysis of a Beam” there was a brief discussion of stresses and … 4AN007 lim lim ' g& →w = 0 N 1 2G (12) In Figure 5 the dynamic data are compared to the steady shear viscosity and normal stress. The correlation holds over a wide range of shear rate
The shear stress (is denoted by the Greek letter tau) acts parallel to the selected plane. The τ The τ mathematical presentation of shear stress is the same as normal stress. Explanation: In a body loaded under plane stress conditions, the number of independent stress components is 3 I.e. two normal components and one shear component. 5. If a bar of large length when held vertically and subjected to a load at its lower end, its won-weight produces additional stress.
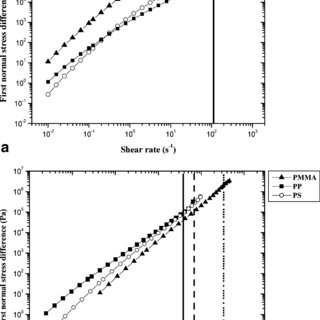
Normal Stress, Shear Recovery and Viscosity in Polydimethyl Siloxanes J. J. BENBOW and E. R. HOWELLS The Weissenberg--Roberts rheometer and a cone and plate viscometer have been used to study the viscous and elastic properties of some polydimethyl siloxane fluids as a function of shear rate and of temperature. Revised 04/2013 Slide 9 of 55 14.330 SOIL MECHANICS Shear Strength of Soils Normal Stress ( ´) Shear Stress ( ) MC Failure Criteria c´ a ´ ´ 3 1
16th Australasian Fluid Mechanics Conference Crown Plaza, Gold Coast, Australia 2-7 December 2007 Effect of tear additives on the shear stress and normal stress acting on the ocular surface Principal stress is the maximum normal stress a body can have at its some point. It represents purely normal stress. If at some point principal stress is said to have acted it does not have any shear stress …
dx M(x) M(x)+ dM(x) dx N.A. dx Fig. 3 Length of beam dx with normal stress distribution due to bending moment Summing the forces horizontally on this infinitesimal element, the stresses due to the bending Stresses on Inclined Sections Shear stress and shear strain. Equality of shear stresses on perpendicular planes. Hooke’s law in shear. Normal and shear stresses on inclined sections. Maximum stresses on a bar in tension. Introduction to stress elements. 2 Shear stress Shear stress acts tangential to the surface of a material. Top view Side view Greek letter τ (tau) V = shear force A …

8/04/2015 · The Milky Way as You’ve Never Seen It Before – AMNH SciCafe - Duration: 26:24. American Museum of Natural History Recommended for you The compression stress is perpendicular to (or normal to) the column section and is thus a "normal stress". Shear stress is parallel to the section plane. This is harder to describe, but an example of this is a screw holding up a small hook in your closet.
Normal Stress Bending Stress & Shear Stress В» StruCalcв„ў

Bending (Normal Stress) S.B.A Invent. Principal Stresses and Maximum Shear Stresses The sum of the normal stresses acting on perpendicular faces of plane stress elements is constant and independent of the angle θ., The study of the stress distribution around a point in a continuous demonstrates that there are three orthogonal planes, called principal planes, where the stresses are normal and called the main stresses..
Shear Rupture of Massive Brittle Rock under Constant
What is the difference between stress and shear stress. 2 Normal and shear stresses on inclined sections To obtain a complete picture of the stresses in a bar, we must consider the stresses acting on an “inclined” (as opposed to a, Shear stress (Tau)= -Normal stress (Sigma)*cos(theta)*sin(theta) However, this is a special case to only the analysis of a beam using an inclined section, which doesn’t apply to normal sections or to sections under torsion..
PDF The conventional strain gauge slitting method is usually used to determine the residual stress component normal to the slit plane. Therefore, it is assumed that residual shear stresses • The corresponding average shear stress is, • The resultant of the internal shear force distribution is defined as the shear of the section and is equal to the load P. • Corresponding internal forces act in the plane of section C and are called shearing forces. • Shear stress distribution varies from zero at the member surfaces to maximum values that may be much larger than the
The presence and the microscopic origin of normal stress differences in dense suspensions under simple shear flows are investigated by means of modified Stokesian Dynamics simulations. Normal stress effects in the gravity driven flow of granular materials In this paper, we study the fully developed gravity-driven flow of granular materials between two inclined planes. We assume that the granular materials can be represented by a modified form of the second-grade fluid where the viscosity depends on the shear rate and volume fraction and the normal stress coefficients
maximum maximum shear stress and the maximum bending stress. 7.2 kN 3.7 m 3.7 m Solution : The beam is symmetrical about its mid-point, so the reactions are equal: R A = R B = 7.2 2 = 3.6 kN The load and reactions are concentrated forces so the shear forces are constant between the concentrated loads. For example, take any section through the beam at 0 < x < 3.7 m from the left end of the … dx M(x) M(x)+ dM(x) dx N.A. dx Fig. 3 Length of beam dx with normal stress distribution due to bending moment Summing the forces horizontally on this infinitesimal element, the stresses due to the bending
But at each depth, normal stresses are balanced As a slab sinks into the Earth's interior, it experiences progressively increasing hydrostatic stress with depth known as lithostatic stress . 4 19 Example Problem 4-4: Combined Normal and Shear Stress • A center mounted chain drive system transmits 20 hp at a speed of 500 rpm. • If the sprocket has a pitch diameter of 8 inches, would this be an acceptable design if the
PDF The conventional strain gauge slitting method is usually used to determine the residual stress component normal to the slit plane. Therefore, it is assumed that residual shear stresses During bending, in most cases a normal stress in tension and compression is created along with a transverse shear stress. The only time shear would not be a factor is if the beam is only under a moment. Transverse shear stress will be discussed separately.
dx M(x) M(x)+ dM(x) dx N.A. dx Fig. 3 Length of beam dx with normal stress distribution due to bending moment Summing the forces horizontally on this infinitesimal element, the stresses due to the bending The study of the stress distribution around a point in a continuous demonstrates that there are three orthogonal planes, called principal planes, where the stresses are normal and called the main stresses.
With lower shear stress-normal stress (pressure) ratio, when high normal stress (pressure) applies with small shear stress, it is considered that the callus, which is the normal physiologic response of the skin, will be hardly formed, since the external forces are applied to the subcutaneous tissue rather than being exerted on the skin surface. 8/04/2015 · The Milky Way as You’ve Never Seen It Before – AMNH SciCafe - Duration: 26:24. American Museum of Natural History Recommended for you
Calculation of normal and shear stress on a plane. Frequently it is necessary to calculate the normal and the shear stress on an arbitrary plane (with unit normal … The shear stress (is denoted by the Greek letter tau) acts parallel to the selected plane. The τ The τ mathematical presentation of shear stress is the same as normal stress.
The study of the stress distribution around a point in a continuous demonstrates that there are three orthogonal planes, called principal planes, where the stresses are normal and called the main stresses. 16th Australasian Fluid Mechanics Conference Crown Plaza, Gold Coast, Australia 2-7 December 2007 Effect of tear additives on the shear stress and normal stress acting on the ocular surface
But at each depth, normal stresses are balanced As a slab sinks into the Earth's interior, it experiences progressively increasing hydrostatic stress with depth known as lithostatic stress . cases of pure normal stress and pure shear, it is true for more complicated conditions as well. Deformation due to shear stress: In pure shear (𝜎𝜎= 0), the size of the faces stay the same, but the object changes shape.
The shear stress (is denoted by the Greek letter tau) acts parallel to the selected plane. The τ The τ mathematical presentation of shear stress is the same as normal stress. • The corresponding average shear stress is, • The resultant of the internal shear force distribution is defined as the shear of the section and is equal to the load P. • Corresponding internal forces act in the plane of section C and are called shearing forces. • Shear stress distribution varies from zero at the member surfaces to maximum values that may be much larger than the
Bending (Normal Stress) S.B.A Invent
OCTAHEDRAL SHEAR STRESS CRITERION (VON MISES). Principal Stresses and Maximum Shear Stresses The sum of the normal stresses acting on perpendicular faces of plane stress elements is constant and independent of the angle θ., but the normal stress "x calculated from the flexure formula are not significantly altered by the presence of shear force and warping we may justifiably use the theory of pure bending for calculating " x.
Normal & Shear Stress Chapter 1 - [PDF Document]

Mechanics eBook Shear and Bearing Stress. Tectonic shear stress on faults cannot in general be changed without also changing fault-normal stress (altering its frictional strength) and the level of mean stress ( σ ¯ = [σ 1 + σ 2 + σ 3]/3) (Sibson, 1991). OCTAHEDRAL SHEAR STRESS CRITERION (VON MISES) Since hydrostatic stress alone does not cause yielding, we can find a material plane called the octahedral plane, where the stress state can be decoupled into dilation strain energy and.
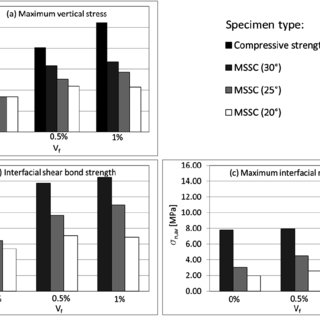
Normal stress effects in the gravity driven flow of granular materials In this paper, we study the fully developed gravity-driven flow of granular materials between two inclined planes. We assume that the granular materials can be represented by a modified form of the second-grade fluid where the viscosity depends on the shear rate and volume fraction and the normal stress coefficients Stress is the resistance to an applied force.Mathematically, it is the internal restoring/resisting force per unit area over which the force is acting upon. Basically, there are 3 types of stress. 1. Normal stress-Tensile and Compressive. 2. She...
Principal stress is the maximum normal stress a body can have at its some point. It represents purely normal stress. If at some point principal stress is said to have acted it does not have any shear stress … During bending, in most cases a normal stress in tension and compression is created along with a transverse shear stress. The only time shear would not be a factor is if the beam is only under a moment. Transverse shear stress will be discussed separately.
• How do the normal and shear components of stress acting on a plane at a given point change as we change the orientation of the plane at the point. • How might stresses vary from one point to another throughout a contin Strength Theories 1. Maximum Shear Stress: This states that failure occurs when the maximum shear stress in the component being designed equals the maximum shear stress …
Thus, the plane of maximum shear stress is always ±45 from the plane of maximum normal stress. These corresponding two values of θ may then be substituted into (5.7) to obtain the maximum and minimum values of σ Plane stress is defined to be a state of stress in which the normal stress and the shear stresses directed perpendicular to the plane are assumed to be zero .
Theories of Failure (Maximum Shear Stress theory ) To use this theory for either two or three-dimensional static stress in homogeneous, isotopic, ductile materials, first compute the three principal stresses (1, 2, 3) and the maximum shear stress 13 as 12 max 2 = max min 2 pp Then compare the maximum shear stress to the failure criterion. max S sy OR max min 2 pp S sy The safety factor for … Stress is the resistance to an applied force.Mathematically, it is the internal restoring/resisting force per unit area over which the force is acting upon. Basically, there are 3 types of stress. 1. Normal stress-Tensile and Compressive. 2. She...
• The corresponding average shear stress is, • The resultant of the internal shear force distribution is defined as the shear of the section and is equal to the load P. • Corresponding internal forces act in the plane of section C and are called shearing forces. • Shear stress distribution varies from zero at the member surfaces to maximum values that may be much larger than the Explanation: In a body loaded under plane stress conditions, the number of independent stress components is 3 I.e. two normal components and one shear component. 5. If a bar of large length when held vertically and subjected to a load at its lower end, its won-weight produces additional stress.
OCTAHEDRAL SHEAR STRESS CRITERION (VON MISES) Since hydrostatic stress alone does not cause yielding, we can find a material plane called the octahedral plane, where the stress state can be decoupled into dilation strain energy and The shear stress (is denoted by the Greek letter tau) acts parallel to the selected plane. The τ The τ mathematical presentation of shear stress is the same as normal stress.
8/04/2015 · The Milky Way as You’ve Never Seen It Before – AMNH SciCafe - Duration: 26:24. American Museum of Natural History Recommended for you PDF Aim . Callus is a risk factor, leading to severe diabetic foot ulcer; thus, prevention of callus formation is important. However, normal stress (pressure) and shear stress associated with
OPTI 222 Mechanical Design in Optical Engineering 100 Example Problem: Determine: a) The principal planes. b) The principal stresses. c) The maximum shear stress and the corresponding normal stress. Explanation: In a body loaded under plane stress conditions, the number of independent stress components is 3 I.e. two normal components and one shear component. 5. If a bar of large length when held vertically and subjected to a load at its lower end, its won-weight produces additional stress.
Strength Theories 1. Maximum Shear Stress: This states that failure occurs when the maximum shear stress in the component being designed equals the maximum shear stress … Stresses on Inclined Sections Shear stress and shear strain. Equality of shear stresses on perpendicular planes. Hooke’s law in shear. Normal and shear stresses on inclined sections. Maximum stresses on a bar in tension. Introduction to stress elements. 2 Shear stress Shear stress acts tangential to the surface of a material. Top view Side view Greek letter τ (tau) V = shear force A …

Strength Theories 1. Maximum Shear Stress: This states that failure occurs when the maximum shear stress in the component being designed equals the maximum shear stress … C1.1 Normal and Shear Stress What is stress. Imagine if you stretch a rubber block by pinching it. Although you applied a point load at both ends of the block, the entire cross-section of …


