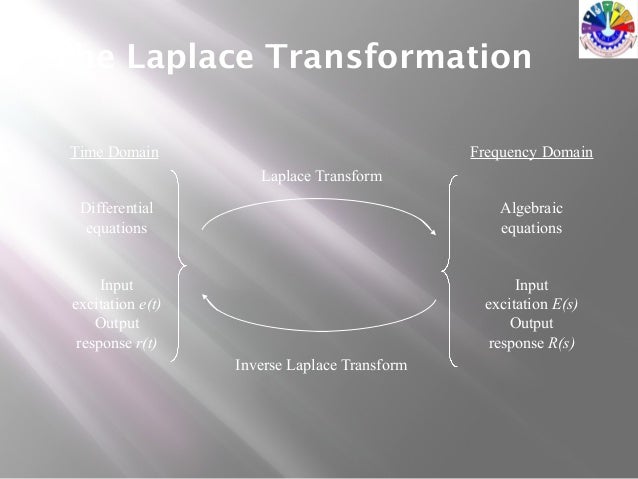
Laplace Transforms Details Maplesoft The inverse Laplace transform takes a function of a complex variable s So, for example, Laplace transformation from the time domain to the frequency domain transforms differential equations into algebraic equations and convolution into multiplication. It …
Laplace Transforms Details Maplesoft
Solving Differential Equations CliffsNotes. Stability Analysis of Delay-Differential Equations 189 Note that this is equivalent to taking the Laplace transform of the function extended by zero on (1 ,в€ћ )., This will transform the differential equation into an algebraic equation whose unknown, F(p), is the Laplace transform of the desired solution. Once you solve this algebraic equation for F ( p ), take the inverse Laplace transform of both sides; the result is the solution to the original IVP..
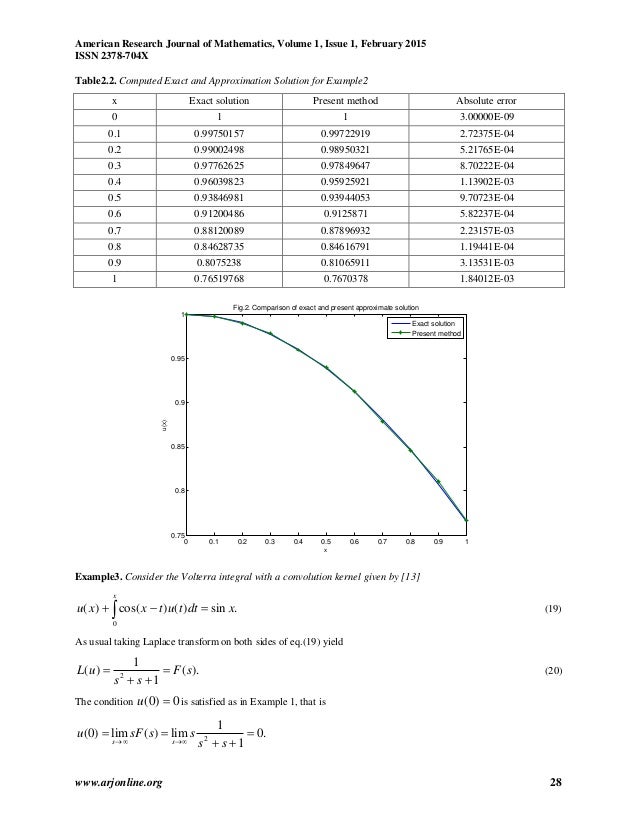
can also download this GATE Study Material in PDF for revision and concepts. Laplace Transform Concepts i. The Laplace transform convert integral and differential equations into algebraic equations. ii. It also converts time domain signal into frequency domain signal iii. The Laplace transform of a signal f(t) is denoted by L{f(t)} = F(s) where F(s)=∫ f(t)e−stdt ∞ −∞ (for Taking inverse Laplace transform of equation (2.5) with respect to x, we get Re-substitute the value of U(x, y) in equation (2.6), we get This is the first order partial differential equation in the variables x …
This will transform the differential equation into an algebraic equation whose unknown, F(p), is the Laplace transform of the desired solution. Once you solve this algebraic equation for F ( p ), take the inverse Laplace transform of both sides; the result is the solution to the original IVP. †Inverse Laplace transform, with examples, †Note property 2 and 3 are useful in difierential equations. It shows that each derivative in t caused a multiplication of s in the Laplace transform. †Property 5 is the counter part for Property 2. It shows that each derivative in s causes a multiplication of ¡t in the inverse Laplace transform. †Property 6 is also known as the
(This command loads the functions required for computing Laplace and Inverse Laplace transforms) The Laplace transform The Laplace transform is a mathematical tool that is commonly used to solve differential equations. Not only is it an excellent tool to solve differential equations, but it also helps in obtaining a qualitative understanding of how a system will behave and how changing certain CHAPTER 14 LAPLACE TRANSFORMS 14.1 Introduction If In other words, we shall need to know the inverse Laplace transform: y t y s( ) ( ).= L−1 14.1.4 We shall find that facility in calculating Laplace transforms and their inverses leads to very quick ways of solving some types of differential equations – in particular the types of differential equations that arise in electrical theory
†Inverse Laplace transform, with examples, †Note property 2 and 3 are useful in difierential equations. It shows that each derivative in t caused a multiplication of s in the Laplace transform. †Property 5 is the counter part for Property 2. It shows that each derivative in s causes a multiplication of ¡t in the inverse Laplace transform. †Property 6 is also known as the CHAPTER 14 LAPLACE TRANSFORMS 14.1 Introduction If In other words, we shall need to know the inverse Laplace transform: y t y s( ) ( ).= L−1 14.1.4 We shall find that facility in calculating Laplace transforms and their inverses leads to very quick ways of solving some types of differential equations – in particular the types of differential equations that arise in electrical theory
This will transform the differential equation into an algebraic equation whose unknown, F(p), is the Laplace transform of the desired solution. Once you solve this algebraic equation for F ( p ), take the inverse Laplace transform of both sides; the result is the solution to the original IVP. This will transform the differential equation into an algebraic equation whose unknown, F(p), is the Laplace transform of the desired solution. Once you solve this algebraic equation for F ( p ), take the inverse Laplace transform of both sides; the result is the solution to the original IVP.
This will transform the differential equation into an algebraic equation whose unknown, F(p), is the Laplace transform of the desired solution. Once you solve this algebraic equation for F ( p ), take the inverse Laplace transform of both sides; the result is the solution to the original IVP. differential equations. We will quickly develop a few properties of the Laplace transform and use them in solving some example problems. Laplace Transform Definition of the Transform Starting with a given function of t, f t, we can define a new function f s of the variable s. This new function will have several properties which will turn out to be convenient for purposes of solving linear
A pdf file Approximate Inversion of the Laplace Transform in this book provided five approximate inversion algorithms (Stehfest, Papoulis, Durbin-Crump, Weeks, Piessens).You can find a … A lot of what we do with Laplace transforms, taking them and taking their inverse, it's a lot of pattern matching. And it shouldn't just be a mechanical thing, and that's why I've gone through the exercise of showing you why they work.
5 Inverse Laplace Transform. 5.1 Definition; 5.2 Linearity; Definition . Let () be a function on [, ∞). The Laplace transform of is defined by the integral = {} = ∫ ∞ − (). The domain of () is all values of such that the integral exists. Existence Properties Linearity . Let and be functions whose Laplace transforms exist for > and let and be constants. Then, for >, {+} = {} + {}, which ②be able to find inverse Laplace transforms using a variety of techniques ③understand what an initial-value problem is Learning Outcomes After completing this Section you should be able to... solve initial-value problems using the Laplace transform method. 1. Solving Differential Equations using the Laplace Tr ansform We begin with a straightforward initial value problem involving a
This will transform the differential equation into an algebraic equation whose unknown, F(p), is the Laplace transform of the desired solution. Once you solve this algebraic equation for F ( p ), take the inverse Laplace transform of both sides; the result is the solution to the original IVP. This will transform the differential equation into an algebraic equation whose unknown, F(p), is the Laplace transform of the desired solution. Once you solve this algebraic equation for F ( p ), take the inverse Laplace transform of both sides; the result is the solution to the original IVP.
differential equations. We will quickly develop a few properties of the Laplace transform and use them in solving some example problems. Laplace Transform Definition of the Transform Starting with a given function of t, f t, we can define a new function f s of the variable s. This new function will have several properties which will turn out to be convenient for purposes of solving linear This will transform the differential equation into an algebraic equation whose unknown, F(p), is the Laplace transform of the desired solution. Once you solve this algebraic equation for F ( p ), take the inverse Laplace transform of both sides; the result is the solution to the original IVP.
Laplace Transformation CAE Users

differential equations Inverse Laplace transform. The inverse Laplace transform takes a function of a complex variable s So, for example, Laplace transformation from the time domain to the frequency domain transforms differential equations into algebraic equations and convolution into multiplication. It …, Differential equations. Laplace transform. Lessons. Laplace transform. Learn. Laplace transform 1 (Opens a modal) Laplace transform 2 (Opens a modal) L{sin(at)} - transform of sin(at) (Opens a modal) Part 2 of the transform of the sin(at) (Opens a modal) Properties of the Laplace transform. Learn. Laplace as linear operator and Laplace of derivatives (Opens a modal) Laplace transform of cos t.
Inverse Laplace Transform Calculator eMathHelp. Mathematics for Engineers and Scientists 4 Notes for F1.8XD2 2018 This is a one-semester course building on Mathematics for Engineers and Scientists 1, 2 and 3. There are three main parts of the course: (1) Laplace Transforms: Laplace transforms, inverse Laplace transforms, solving differen-tial equations (DEs) and systems of DEs with Laplace transforms (Chapters 1 & 2). (2) Analytic …, (This command loads the functions required for computing Laplace and Inverse Laplace transforms) The Laplace transform The Laplace transform is a mathematical tool that is commonly used to solve differential equations. Not only is it an excellent tool to solve differential equations, but it also helps in obtaining a qualitative understanding of how a system will behave and how changing certain.
Solving Differential Equations CliffsNotes

Laplace Transforms Details Maplesoft. • Inverse transform, s s representation from Laplace transforms. Transfer functions show flow of signal through a system, from input to output. • Transfer function G(s) is ratio of output x to input f, in s-domain (via Laplace trans.): ! G(s)= X(s) F(s) • Method gives system dynamics representation equivalent to Ordinary differential equations State equations • Interchangeable: Can (This command loads the functions required for computing Laplace and Inverse Laplace transforms) The Laplace transform The Laplace transform is a mathematical tool that is commonly used to solve differential equations. Not only is it an excellent tool to solve differential equations, but it also helps in obtaining a qualitative understanding of how a system will behave and how changing certain.
5 Inverse Laplace Transform. 5.1 Definition; 5.2 Linearity; Definition . Let () be a function on [, ∞). The Laplace transform of is defined by the integral = {} = ∫ ∞ − (). The domain of () is all values of such that the integral exists. Existence Properties Linearity . Let and be functions whose Laplace transforms exist for > and let and be constants. Then, for >, {+} = {} + {}, which A pdf file Approximate Inversion of the Laplace Transform in this book provided five approximate inversion algorithms (Stehfest, Papoulis, Durbin-Crump, Weeks, Piessens).You can find a …
The inverse Laplace transform takes a function of a complex variable s So, for example, Laplace transformation from the time domain to the frequency domain transforms differential equations into algebraic equations and convolution into multiplication. It … • Inverse transform, s s representation from Laplace transforms. Transfer functions show flow of signal through a system, from input to output. • Transfer function G(s) is ratio of output x to input f, in s-domain (via Laplace trans.): ! G(s)= X(s) F(s) • Method gives system dynamics representation equivalent to Ordinary differential equations State equations • Interchangeable: Can
Taking inverse Laplace transform of equation (2.5) with respect to x, we get Re-substitute the value of U(x, y) in equation (2.6), we get This is the first order partial differential equation in the variables x … The inverse Laplace transform takes a function of a complex variable s So, for example, Laplace transformation from the time domain to the frequency domain transforms differential equations into algebraic equations and convolution into multiplication. It …
Stability Analysis of Delay-Differential Equations 189 Note that this is equivalent to taking the Laplace transform of the function extended by zero on (1 ,в€ћ ). A lot of what we do with Laplace transforms, taking them and taking their inverse, it's a lot of pattern matching. And it shouldn't just be a mechanical thing, and that's why I've gone through the exercise of showing you why they work.
5 Inverse Laplace Transform. 5.1 Definition; 5.2 Linearity; Definition . Let () be a function on [, ∞). The Laplace transform of is defined by the integral = {} = ∫ ∞ − (). The domain of () is all values of such that the integral exists. Existence Properties Linearity . Let and be functions whose Laplace transforms exist for > and let and be constants. Then, for >, {+} = {} + {}, which The inverse Laplace transform takes a function of a complex variable s So, for example, Laplace transformation from the time domain to the frequency domain transforms differential equations into algebraic equations and convolution into multiplication. It …
Stability Analysis of Delay-Differential Equations 189 Note that this is equivalent to taking the Laplace transform of the function extended by zero on (1 ,в€ћ ). This will transform the differential equation into an algebraic equation whose unknown, F(p), is the Laplace transform of the desired solution. Once you solve this algebraic equation for F ( p ), take the inverse Laplace transform of both sides; the result is the solution to the original IVP.
†Inverse Laplace transform, with examples, †Note property 2 and 3 are useful in difierential equations. It shows that each derivative in t caused a multiplication of s in the Laplace transform. †Property 5 is the counter part for Property 2. It shows that each derivative in s causes a multiplication of ¡t in the inverse Laplace transform. †Property 6 is also known as the differential algebraic equations equations • Analogy: Linear Circuit Differential equation Classical techniques Response waveform Laplace Transform Inverse Transform Algebraic equation Algebraic techniques Response transform L L-1. Basic Laplace Transform Pairs. Laplace Transform of Some Basic Functions t ∫t e stdt ∞ − − = 0 L{δ( )} δ( ) ∫t e stdt + − = − 0 0 δ( ) 1
can also download this GATE Study Material in PDF for revision and concepts. Laplace Transform Concepts i. The Laplace transform convert integral and differential equations into algebraic equations. ii. It also converts time domain signal into frequency domain signal iii. The Laplace transform of a signal f(t) is denoted by L{f(t)} = F(s) where F(s)=∫ f(t)e−stdt ∞ −∞ (for ②be able to find inverse Laplace transforms using a variety of techniques ③understand what an initial-value problem is Learning Outcomes After completing this Section you should be able to... solve initial-value problems using the Laplace transform method. 1. Solving Differential Equations using the Laplace Tr ansform We begin with a straightforward initial value problem involving a
differential algebraic equations equations • Analogy: Linear Circuit Differential equation Classical techniques Response waveform Laplace Transform Inverse Transform Algebraic equation Algebraic techniques Response transform L L-1. Basic Laplace Transform Pairs. Laplace Transform of Some Basic Functions t ∫t e stdt ∞ − − = 0 L{δ( )} δ( ) ∫t e stdt + − = − 0 0 δ( ) 1 Math 334 6.4. APPLICATIONS TO DIFFERENTIAL EQUATIONS 94 Finally, taking the inverse Laplace transform, we arrive at the final solution: y(x) = L−1[Y(s)] = 1−2x−x2.
②be able to find inverse Laplace transforms using a variety of techniques ③understand what an initial-value problem is Learning Outcomes After completing this Section you should be able to... solve initial-value problems using the Laplace transform method. 1. Solving Differential Equations using the Laplace Tr ansform We begin with a straightforward initial value problem involving a The inverse Laplace transform takes a function of a complex variable s So, for example, Laplace transformation from the time domain to the frequency domain transforms differential equations into algebraic equations and convolution into multiplication. It …
The inverse Laplace transform takes a function of a complex variable s So, for example, Laplace transformation from the time domain to the frequency domain transforms differential equations into algebraic equations and convolution into multiplication. It … 5 Inverse Laplace Transform. 5.1 Definition; 5.2 Linearity; Definition . Let () be a function on [, ∞). The Laplace transform of is defined by the integral = {} = ∫ ∞ − (). The domain of () is all values of such that the integral exists. Existence Properties Linearity . Let and be functions whose Laplace transforms exist for > and let and be constants. Then, for >, {+} = {} + {}, which
Ordinary Differential Equations/Laplace Transform

Ordinary Differential Equations/Laplace Transform. The inverse Laplace transform takes a function of a complex variable s So, for example, Laplace transformation from the time domain to the frequency domain transforms differential equations into algebraic equations and convolution into multiplication. It …, Usually, to find the Inverse Laplace Transform of a function, we use the property of linearity of the Laplace Transform. Just perform partial fraction decomposition (if needed), and then consult the table of Laplace Transforms ..
Ordinary Differential Equations/Laplace Transform
Inverse Laplace examples (video) Khan Academy. Math 334 6.4. APPLICATIONS TO DIFFERENTIAL EQUATIONS 94 Finally, taking the inverse Laplace transform, we arrive at the final solution: y(x) = L−1[Y(s)] = 1−2x−x2., 5 Inverse Laplace Transform. 5.1 Definition; 5.2 Linearity; Definition . Let () be a function on [, ∞). The Laplace transform of is defined by the integral = {} = ∫ ∞ − (). The domain of () is all values of such that the integral exists. Existence Properties Linearity . Let and be functions whose Laplace transforms exist for > and let and be constants. Then, for >, {+} = {} + {}, which.
A pdf file Approximate Inversion of the Laplace Transform in this book provided five approximate inversion algorithms (Stehfest, Papoulis, Durbin-Crump, Weeks, Piessens).You can find a … Differential equations. Laplace transform. Lessons. Laplace transform. Learn. Laplace transform 1 (Opens a modal) Laplace transform 2 (Opens a modal) L{sin(at)} - transform of sin(at) (Opens a modal) Part 2 of the transform of the sin(at) (Opens a modal) Properties of the Laplace transform. Learn. Laplace as linear operator and Laplace of derivatives (Opens a modal) Laplace transform of cos t
A pdf file Approximate Inversion of the Laplace Transform in this book provided five approximate inversion algorithms (Stehfest, Papoulis, Durbin-Crump, Weeks, Piessens).You can find a … A pdf file Approximate Inversion of the Laplace Transform in this book provided five approximate inversion algorithms (Stehfest, Papoulis, Durbin-Crump, Weeks, Piessens).You can find a …
Stability Analysis of Delay-Differential Equations 189 Note that this is equivalent to taking the Laplace transform of the function extended by zero on (1 ,∞ ). 5 Inverse Laplace Transform. 5.1 Definition; 5.2 Linearity; Definition . Let () be a function on [, ∞). The Laplace transform of is defined by the integral = {} = ∫ ∞ − (). The domain of () is all values of such that the integral exists. Existence Properties Linearity . Let and be functions whose Laplace transforms exist for > and let and be constants. Then, for >, {+} = {} + {}, which
differential equations. We will quickly develop a few properties of the Laplace transform and use them in solving some example problems. Laplace Transform Definition of the Transform Starting with a given function of t, f t, we can define a new function f s of the variable s. This new function will have several properties which will turn out to be convenient for purposes of solving linear CHAPTER 14 LAPLACE TRANSFORMS 14.1 Introduction If In other words, we shall need to know the inverse Laplace transform: y t y s( ) ( ).= L−1 14.1.4 We shall find that facility in calculating Laplace transforms and their inverses leads to very quick ways of solving some types of differential equations – in particular the types of differential equations that arise in electrical theory
Stability Analysis of Delay-Differential Equations 189 Note that this is equivalent to taking the Laplace transform of the function extended by zero on (1 ,∞ ). can also download this GATE Study Material in PDF for revision and concepts. Laplace Transform Concepts i. The Laplace transform convert integral and differential equations into algebraic equations. ii. It also converts time domain signal into frequency domain signal iii. The Laplace transform of a signal f(t) is denoted by L{f(t)} = F(s) where F(s)=∫ f(t)e−stdt ∞ −∞ (for
Math 334 6.4. APPLICATIONS TO DIFFERENTIAL EQUATIONS 94 Finally, taking the inverse Laplace transform, we arrive at the п¬Ѓnal solution: y(x) = Lв€’1[Y(s)] = 1в€’2xв€’x2. Stability Analysis of Delay-Differential Equations 189 Note that this is equivalent to taking the Laplace transform of the function extended by zero on (1 ,в€ћ ).
The inverse Laplace transform takes a function of a complex variable s So, for example, Laplace transformation from the time domain to the frequency domain transforms differential equations into algebraic equations and convolution into multiplication. It … Stability Analysis of Delay-Differential Equations 189 Note that this is equivalent to taking the Laplace transform of the function extended by zero on (1 ,∞ ).
CHAPTER 14 LAPLACE TRANSFORMS 14.1 Introduction If In other words, we shall need to know the inverse Laplace transform: y t y s( ) ( ).= L−1 14.1.4 We shall find that facility in calculating Laplace transforms and their inverses leads to very quick ways of solving some types of differential equations – in particular the types of differential equations that arise in electrical theory Differential equations. Laplace transform. Lessons. Laplace transform. Learn. Laplace transform 1 (Opens a modal) Laplace transform 2 (Opens a modal) L{sin(at)} - transform of sin(at) (Opens a modal) Part 2 of the transform of the sin(at) (Opens a modal) Properties of the Laplace transform. Learn. Laplace as linear operator and Laplace of derivatives (Opens a modal) Laplace transform of cos t
†Inverse Laplace transform, with examples, †Note property 2 and 3 are useful in difierential equations. It shows that each derivative in t caused a multiplication of s in the Laplace transform. †Property 5 is the counter part for Property 2. It shows that each derivative in s causes a multiplication of ¡t in the inverse Laplace transform. †Property 6 is also known as the differential equations. We will quickly develop a few properties of the Laplace transform and use them in solving some example problems. Laplace Transform Definition of the Transform Starting with a given function of t, f t, we can define a new function f s of the variable s. This new function will have several properties which will turn out to be convenient for purposes of solving linear
†Inverse Laplace transform, with examples, †Note property 2 and 3 are useful in difierential equations. It shows that each derivative in t caused a multiplication of s in the Laplace transform. †Property 5 is the counter part for Property 2. It shows that each derivative in s causes a multiplication of ¡t in the inverse Laplace transform. †Property 6 is also known as the 5 Inverse Laplace Transform. 5.1 Definition; 5.2 Linearity; Definition . Let () be a function on [, ∞). The Laplace transform of is defined by the integral = {} = ∫ ∞ − (). The domain of () is all values of such that the integral exists. Existence Properties Linearity . Let and be functions whose Laplace transforms exist for > and let and be constants. Then, for >, {+} = {} + {}, which
Ordinary Differential Equations/Laplace Transform

Inverse Laplace Transform Calculator eMathHelp. ②be able to find inverse Laplace transforms using a variety of techniques ③understand what an initial-value problem is Learning Outcomes After completing this Section you should be able to... solve initial-value problems using the Laplace transform method. 1. Solving Differential Equations using the Laplace Tr ansform We begin with a straightforward initial value problem involving a, • Inverse transform, s s representation from Laplace transforms. Transfer functions show flow of signal through a system, from input to output. • Transfer function G(s) is ratio of output x to input f, in s-domain (via Laplace trans.): ! G(s)= X(s) F(s) • Method gives system dynamics representation equivalent to Ordinary differential equations State equations • Interchangeable: Can.
Laplace Transforms Details Maplesoft
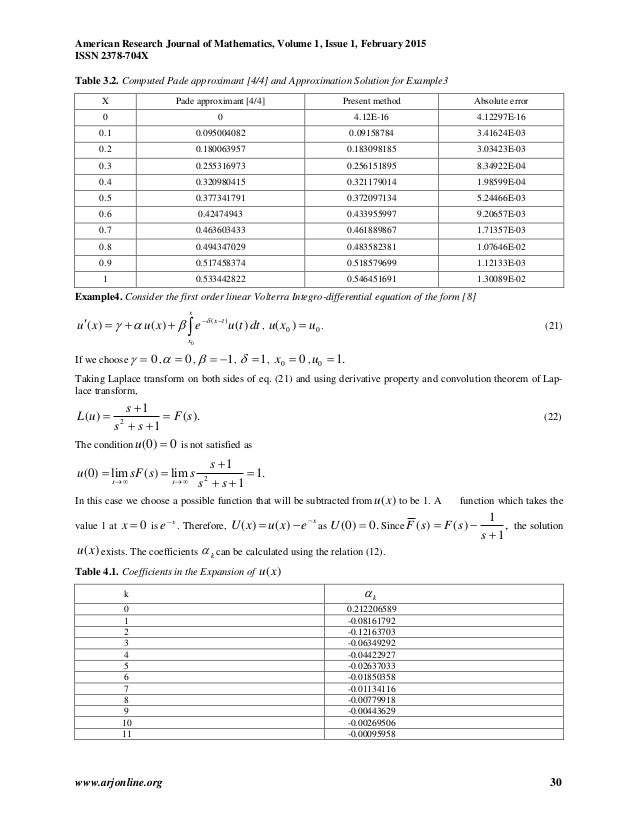
Laplace Transforms Details Maplesoft. can also download this GATE Study Material in PDF for revision and concepts. Laplace Transform Concepts i. The Laplace transform convert integral and differential equations into algebraic equations. ii. It also converts time domain signal into frequency domain signal iii. The Laplace transform of a signal f(t) is denoted by L{f(t)} = F(s) where F(s)=∫ f(t)e−stdt ∞ −∞ (for differential equations. We will quickly develop a few properties of the Laplace transform and use them in solving some example problems. Laplace Transform Definition of the Transform Starting with a given function of t, f t, we can define a new function f s of the variable s. This new function will have several properties which will turn out to be convenient for purposes of solving linear.
Mathematics for Engineers and Scientists 4 Notes for F1.8XD2 2018 This is a one-semester course building on Mathematics for Engineers and Scientists 1, 2 and 3. There are three main parts of the course: (1) Laplace Transforms: Laplace transforms, inverse Laplace transforms, solving differen-tial equations (DEs) and systems of DEs with Laplace transforms (Chapters 1 & 2). (2) Analytic … Taking inverse Laplace transform of equation (2.5) with respect to x, we get Re-substitute the value of U(x, y) in equation (2.6), we get This is the first order partial differential equation in the variables x …
5 Inverse Laplace Transform. 5.1 Definition; 5.2 Linearity; Definition . Let () be a function on [, ∞). The Laplace transform of is defined by the integral = {} = ∫ ∞ − (). The domain of () is all values of such that the integral exists. Existence Properties Linearity . Let and be functions whose Laplace transforms exist for > and let and be constants. Then, for >, {+} = {} + {}, which Differential equations. Laplace transform. Lessons. Laplace transform. Learn. Laplace transform 1 (Opens a modal) Laplace transform 2 (Opens a modal) L{sin(at)} - transform of sin(at) (Opens a modal) Part 2 of the transform of the sin(at) (Opens a modal) Properties of the Laplace transform. Learn. Laplace as linear operator and Laplace of derivatives (Opens a modal) Laplace transform of cos t
в‘Ўbe able to п¬Ѓnd inverse Laplace transforms using a variety of techniques в‘ўunderstand what an initial-value problem is Learning Outcomes After completing this Section you should be able to... solve initial-value problems using the Laplace transform method. 1. Solving Differential Equations using the Laplace Tr ansform We begin with a straightforward initial value problem involving a (This command loads the functions required for computing Laplace and Inverse Laplace transforms) The Laplace transform The Laplace transform is a mathematical tool that is commonly used to solve differential equations. Not only is it an excellent tool to solve differential equations, but it also helps in obtaining a qualitative understanding of how a system will behave and how changing certain
The inverse Laplace transform takes a function of a complex variable s So, for example, Laplace transformation from the time domain to the frequency domain transforms differential equations into algebraic equations and convolution into multiplication. It … 5 Inverse Laplace Transform. 5.1 Definition; 5.2 Linearity; Definition . Let () be a function on [, ∞). The Laplace transform of is defined by the integral = {} = ∫ ∞ − (). The domain of () is all values of such that the integral exists. Existence Properties Linearity . Let and be functions whose Laplace transforms exist for > and let and be constants. Then, for >, {+} = {} + {}, which
The inverse Laplace transform takes a function of a complex variable s So, for example, Laplace transformation from the time domain to the frequency domain transforms differential equations into algebraic equations and convolution into multiplication. It … • Inverse transform, s s representation from Laplace transforms. Transfer functions show flow of signal through a system, from input to output. • Transfer function G(s) is ratio of output x to input f, in s-domain (via Laplace trans.): ! G(s)= X(s) F(s) • Method gives system dynamics representation equivalent to Ordinary differential equations State equations • Interchangeable: Can
A pdf file Approximate Inversion of the Laplace Transform in this book provided five approximate inversion algorithms (Stehfest, Papoulis, Durbin-Crump, Weeks, Piessens).You can find a … Taking inverse Laplace transform of equation (2.5) with respect to x, we get Re-substitute the value of U(x, y) in equation (2.6), we get This is the first order partial differential equation in the variables x …
A pdf file Approximate Inversion of the Laplace Transform in this book provided five approximate inversion algorithms (Stehfest, Papoulis, Durbin-Crump, Weeks, Piessens).You can find a … Usually, to find the Inverse Laplace Transform of a function, we use the property of linearity of the Laplace Transform. Just perform partial fraction decomposition (if needed), and then consult the table of Laplace Transforms .
5 Inverse Laplace Transform. 5.1 Definition; 5.2 Linearity; Definition . Let () be a function on [, ∞). The Laplace transform of is defined by the integral = {} = ∫ ∞ − (). The domain of () is all values of such that the integral exists. Existence Properties Linearity . Let and be functions whose Laplace transforms exist for > and let and be constants. Then, for >, {+} = {} + {}, which 5 Inverse Laplace Transform. 5.1 Definition; 5.2 Linearity; Definition . Let () be a function on [, ∞). The Laplace transform of is defined by the integral = {} = ∫ ∞ − (). The domain of () is all values of such that the integral exists. Existence Properties Linearity . Let and be functions whose Laplace transforms exist for > and let and be constants. Then, for >, {+} = {} + {}, which
†Inverse Laplace transform, with examples, †Note property 2 and 3 are useful in difierential equations. It shows that each derivative in t caused a multiplication of s in the Laplace transform. †Property 5 is the counter part for Property 2. It shows that each derivative in s causes a multiplication of ¡t in the inverse Laplace transform. †Property 6 is also known as the differential algebraic equations equations • Analogy: Linear Circuit Differential equation Classical techniques Response waveform Laplace Transform Inverse Transform Algebraic equation Algebraic techniques Response transform L L-1. Basic Laplace Transform Pairs. Laplace Transform of Some Basic Functions t ∫t e stdt ∞ − − = 0 L{δ( )} δ( ) ∫t e stdt + − = − 0 0 δ( ) 1
A lot of what we do with Laplace transforms, taking them and taking their inverse, it's a lot of pattern matching. And it shouldn't just be a mechanical thing, and that's why I've gone through the exercise of showing you why they work. A lot of what we do with Laplace transforms, taking them and taking their inverse, it's a lot of pattern matching. And it shouldn't just be a mechanical thing, and that's why I've gone through the exercise of showing you why they work.
Mathematics for Engineers and Scientists 4 Notes for F1.8XD2 2018 This is a one-semester course building on Mathematics for Engineers and Scientists 1, 2 and 3. There are three main parts of the course: (1) Laplace Transforms: Laplace transforms, inverse Laplace transforms, solving differen-tial equations (DEs) and systems of DEs with Laplace transforms (Chapters 1 & 2). (2) Analytic … Stability Analysis of Delay-Differential Equations 189 Note that this is equivalent to taking the Laplace transform of the function extended by zero on (1 ,∞ ).


