The ACT Math Test Amazon S3 Trainer/Instructor Notes: Similarity Magnification Ratio Geometry Module 8-1 Unit 8 – Similarity and Trigonometry Magnification Ratio Overview: In this activity participants use coordinate geometry, distance, angle
Unit 8 – Similarity and Trigonometry Magnification Ratio
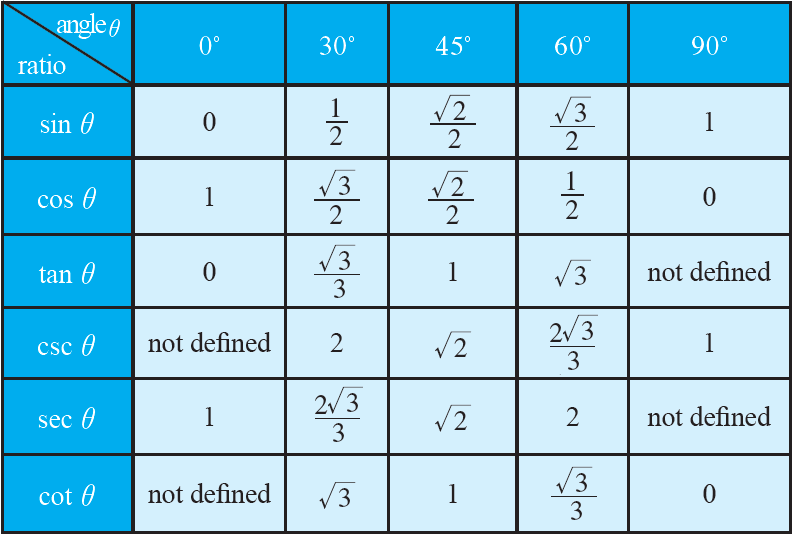
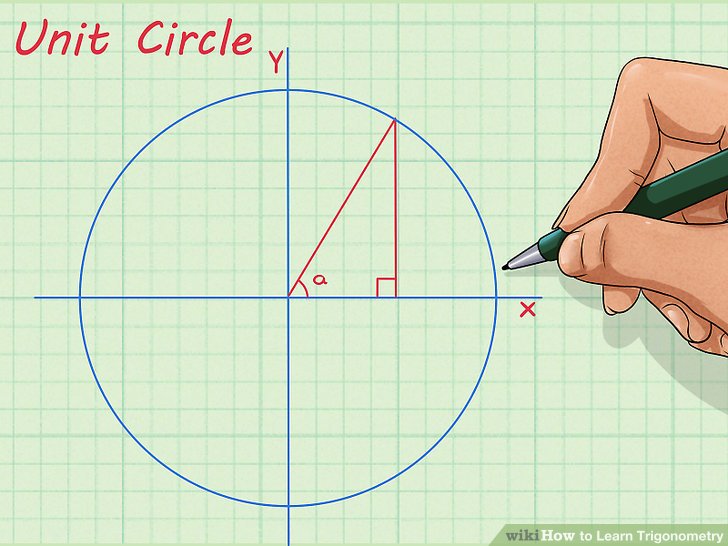
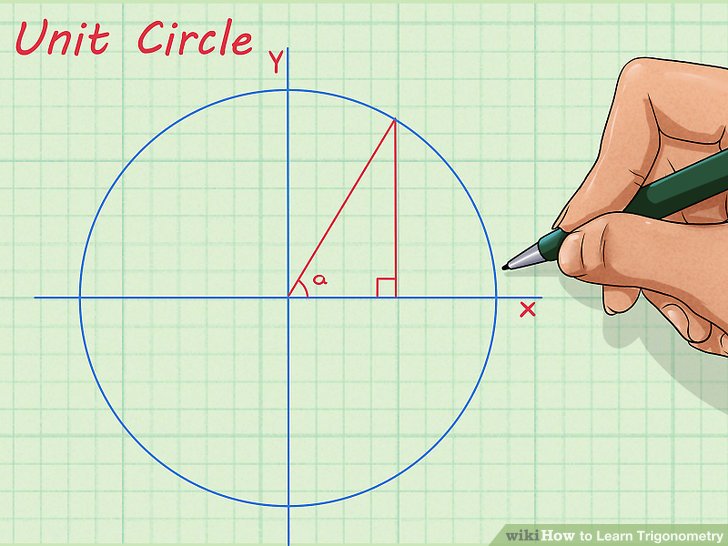
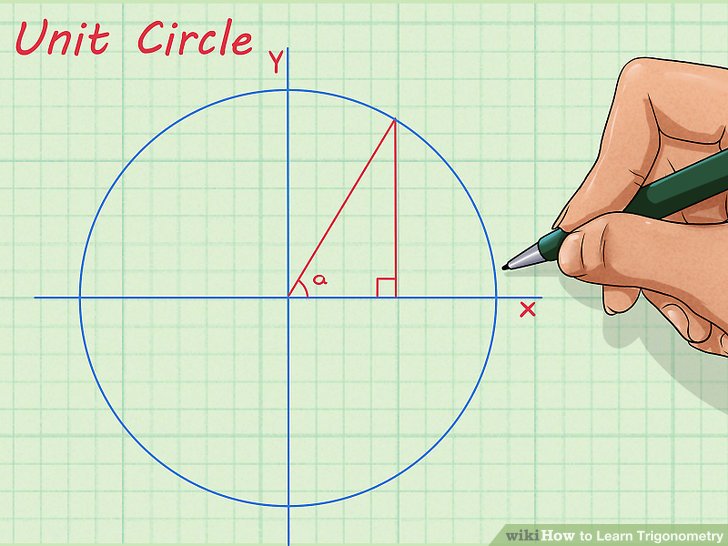
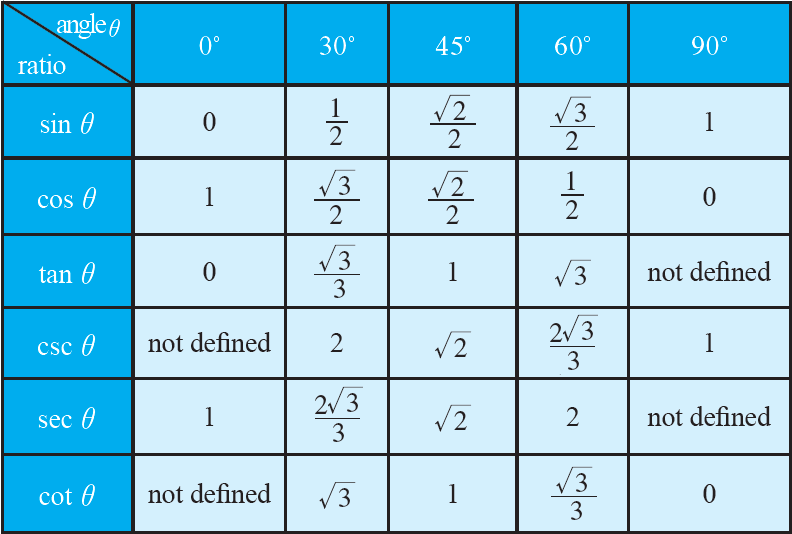
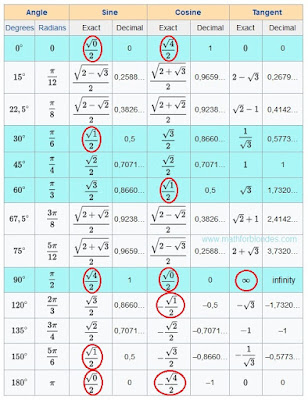
Copyright В© 2010 Pearson Canada Inc. Toronto Ontario.. Right Angle - An angle that is 90 degrees (often represented with the letter C) Acute Angle - An angle that is less than 90 degrees (often represented with letters A and B) Hypotenuse - The side of a right triangle that is across from (opposite) the right angle (often represented, Unit Circle Trigonometry Labeling Special Angles on the Unit Circle Labeling Special Angles on the Unit Circle We are going to deal primarily with special angles around the unit circle, namely the multiples of 30o, 45o, 60o, and 90o. All angles throughout this unit will be drawn in standard position. First, we will draw a unit circle and label the angles that are multiples of 90o. These angles.
to form a triangle (they form a triangle if and only if the sum of any two of them is greater than the third). But if one can form a triangle, then the angles of that triangle are indeed In each case, the trigonometric ratio and its relationship to an acute angle is established in the introductory lesson and then this relationship is applied to determine the lengths of sides in a right triangle in a follow-up lesson.
The ACT Math Test assesses the mathematical skills students are expected to obtain before grade 12 (meaning through advanced algebra and basic trigonometry, but not calculus). For angles that are obtuse (angle is greater than 90°) or negative, we use the following trigonometric ratios. The x and y variables are the values of the x and y coordinates, respectively. The r variable represents the distance from the origin, to the point (x,y). This value can …
demonstrate an understanding of factoring polynomials of degree greater than 2 demonstrate an understanding of angles in standard position, expressed in degrees and radians develop and apply the equation of the unit circle solve problems, using the six trigonometric ratios for angles expressed in radians and degrees graph and analyze the trigonometric functions sine, cosine, and tangent to For angles that are obtuse (angle is greater than 90°) or negative, we use the following trigonometric ratios. The x and y variables are the values of the x and y coordinates, respectively. The r variable represents the distance from the origin, to the point (x,y). This value can …
Definition 2.1: Trigonometric Functions of a General Angle Let Оё be an angle in standard position and suppose that ( x , y ) is any point other than ( 0 , 0 ) on the terminal side of Оё (Figure 2.3). Definition 2.1: Trigonometric Functions of a General Angle Let Оё be an angle in standard position and suppose that ( x , y ) is any point other than ( 0 , 0 ) on the terminal side of Оё (Figure 2.3).
The ACT Math Test assesses the mathematical skills students are expected to obtain before grade 12 (meaning through advanced algebra and basic trigonometry, but not calculus). early astronomers found it necessary to solve for unknown sides and angles of triangles. The Greek astronomer Hipparchus (190-120 B.C.E) began a list of trigonometric ratios to aid in this endeavor.
SAW BLADE ANGLES Measurement and Application of Dihedral Angles The table and blade of a saw represent two planes, but the method of measuring the dihedral angle between them must be modified. •find solutions of trigonometric equations •use trigonometric identities in the solution of trigonometric equations Contents 1. Introduction 2 2. Some special angles and their trigonometric ratios 2 3. Some simple trigonometric equations 2 4. Using identities in the solution of equations 8 5. Some examples where the interval is given in radians 10 www.mathcentre.ac.uk 1 c mathcentre 2009
Definition 2.1: Trigonometric Functions of a General Angle Let Оё be an angle in standard position and suppose that ( x , y ) is any point other than ( 0 , 0 ) on the terminal side of Оё (Figure 2.3). The student, given a point other than the origin on the terminal side of an angle, will use the definitions of the six trigonometric functions to find the sine, cosine, tangent, cotangent, secant, and cosecant of the angle in standard position.
trig functions of given angles, we have been able to find the values of those functions in quadrant II. θ x y r O (x,y) θ O (-4,3) 5. Trig in Four Quadrants Page 4 To expand our knowledge, let’s look at the signs of the coordinates in the four quadrants. x values to the left of the y axis are negative; those to the right are positive. y values below the x axis are negative; those above are Trainer/Instructor Notes: Similarity Magnification Ratio Geometry Module 8-1 Unit 8 – Similarity and Trigonometry Magnification Ratio Overview: In this activity participants use coordinate geometry, distance, angle
•find solutions of trigonometric equations •use trigonometric identities in the solution of trigonometric equations Contents 1. Introduction 2 2. Some special angles and their trigonometric ratios 2 3. Some simple trigonometric equations 2 4. Using identities in the solution of equations 8 5. Some examples where the interval is given in radians 10 www.mathcentre.ac.uk 1 c mathcentre 2009 incident angle at the water-air interface is now larger than the critical angle. This This phenomenon of total internal reflection is used to trap light in fibers.
Definition 2.1: Trigonometric Functions of a General Angle Let Оё be an angle in standard position and suppose that ( x , y ) is any point other than ( 0 , 0 ) on the terminal side of Оё (Figure 2.3). Definition 2.1: Trigonometric Functions of a General Angle Let Оё be an angle in standard position and suppose that ( x , y ) is any point other than ( 0 , 0 ) on the terminal side of Оё (Figure 2.3).
Exact trig ratios of important angles Kuta Software LLC
The ACT Math Test Amazon S3. - Trigonometric ratios - Finding angles - Finding lengths of sidest Glossary - Page 37 Assessment - Page 38 . Maths Module 4 : Geometry and Trigonometry - page 2 Example - Find angles a and b, giving reasons for your answer. a and 25o are corresponding angles, so a = 25o. 80o and b are co-interior angles, so: 80o + b = 180o, b = 180o - 80o = 100o. 1. Shapes 1.1 Angles You will probably, Exact Trig Values of Special Angles Date_____ Period____ Find the exact value of each trigonometric function. 1) tan Оё x y 60 В° 2) sin Оё x y 225 В° 3) sin Оё x y 90 В° 4) cos Оё.
CHAPTER 21 NAVIGATIONAL MATHEMATICS
Trigonometry Tutorial Nipissing University. www.math30.ca Trigonometry LESSON SEVEN- Trigonometric Identities II Lesson Notes Write each expression as a single trigonometric ratio. a) c) b) Example 2 Sum and Difference Identities Contents Subject aims and general information Important symbols and abbreviations Module 1: Equations, manipulation and word problems 1.1 Factorising the sum ofand difference between two cubes.
incident angle at the water-air interface is now larger than the critical angle. This This phenomenon of total internal reflection is used to trap light in fibers. In trigonometry, angles are represented by the Greek letter theta (Оё). The sine of an angle Оё, abbreviated as sin Оё, is the ratio expressed when the side of a right triangle opposite the angle
trig functions of given angles, we have been able to find the values of those functions in quadrant II. θ x y r O (x,y) θ O (-4,3) 5. Trig in Four Quadrants Page 4 To expand our knowledge, let’s look at the signs of the coordinates in the four quadrants. x values to the left of the y axis are negative; those to the right are positive. y values below the x axis are negative; those above are The student, given a point other than the origin on the terminal side of an angle, will use the definitions of the six trigonometric functions to find the sine, cosine, tangent, cotangent, secant, and cosecant of the angle in standard position.
Unit Circle Trigonometry Labeling Special Angles on the Unit Circle Labeling Special Angles on the Unit Circle We are going to deal primarily with special angles around the unit circle, namely the multiples of 30o, 45o, 60o, and 90o. All angles throughout this unit will be drawn in standard position. First, we will draw a unit circle and label the angles that are multiples of 90o. These angles Trigonometric identities and geometry. A C B b) If A = 32В° and B = 89В°, what is the value of C? a) Show that Example 18 . www.math30.ca Trigonometry LESSON SEVEN - Trigonometric Identities II Lesson Notes Solve for x. Round your answer to the nearest tenth. 57 176 153 104 A B x Example 19 Trigonometric identities and geometry. www.math30.ca Trigonometry LESSON SEVEN- Trigonometric Identities
Contents Subject aims and general information Important symbols and abbreviations Module 1: Equations, manipulation and word problems 1.1 Factorising the sum ofand difference between two cubes trigonometric ratios, one for each of the six ways that the sides of the triangle can be compared two at a time. These ratios are called sine, cosine, tangent, cosecant, secant,
•find solutions of trigonometric equations •use trigonometric identities in the solution of trigonometric equations Contents 1. Introduction 2 2. Some special angles and their trigonometric ratios 2 3. Some simple trigonometric equations 2 4. Using identities in the solution of equations 8 5. Some examples where the interval is given in radians 10 www.mathcentre.ac.uk 1 c mathcentre 2009 trigonometric ratios, one for each of the six ways that the sides of the triangle can be compared two at a time. These ratios are called sine, cosine, tangent, cosecant, secant,
The Mathematics Test is a 60-question, 60-minute examination that measures mathematics reasoning abilities. The test focuses on the solution of practical quantitative problems that are An obtuse angle is one greater than a right angle (90В°) but less than 180В°. A straight angle is one whose sides form a continuous straight line (180В°). A reflex angle is one greater than a straight angle (180В°) but less than a circle (360В°). Any two lines meeting at a point form two angles, one less than a straight angle of 180В°(unless exactly a straight angle) and the other greater than
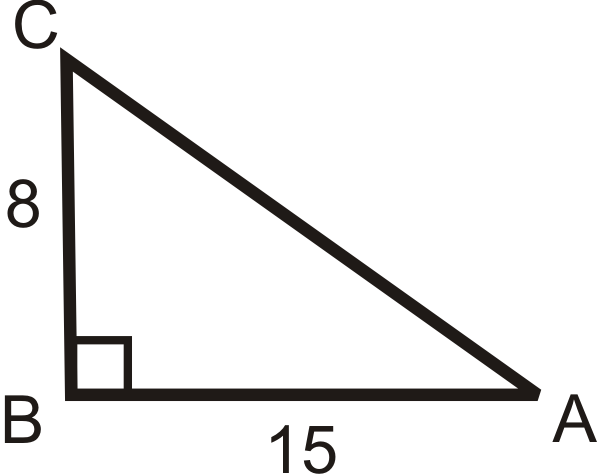
•find solutions of trigonometric equations •use trigonometric identities in the solution of trigonometric equations Contents 1. Introduction 2 2. Some special angles and their trigonometric ratios 2 3. Some simple trigonometric equations 2 4. Using identities in the solution of equations 8 5. Some examples where the interval is given in radians 10 www.mathcentre.ac.uk 1 c mathcentre 2009 Geometry Notes – Chapter 7: Right Triangles Chapter 7 Notes: Right Triangles Page 1 of 3 7.1 – The Pythagorean Theorem . The Pythagorean Theorem . In a right triangle, the square of the length of the hypotenuse is equal to the sum of the squares of the lengths of the legs. Pythagorean Triples – A set of three integers a, b and c that satisfy the equation . ab c22+= 2. 7.2 – Converse of
Solving trigonometric equations she loves math solving sinusoidal equations of the form sin x d khan academy trigonometric functions of angles greater than 360 degrees trigonometric equations review article khan academy Solving Trigonometric Equations She Loves Math Solving Sinusoidal Equations Of The Form Sin X D Khan Academy Trigonometric Functions Of Angles Greater Than 360 … The student, given a point other than the origin on the terminal side of an angle, will use the definitions of the six trigonometric functions to find the sine, cosine, tangent, cotangent, secant, and cosecant of the angle in standard position.
An obtuse angle is one greater than a right angle (90В°) but less than 180В°. A straight angle is one whose sides form a continuous straight line (180В°). A reflex angle is one greater than a straight angle (180В°) but less than a circle (360В°). Any two lines meeting at a point form two angles, one less than a straight angle of 180В°(unless exactly a straight angle) and the other greater than The Mathematics Test is a 60-question, 60-minute examination that measures mathematics reasoning abilities. The test focuses on the solution of practical quantitative problems that are
itself, all angles are necessarily less than 90 . We now extend the definitions of the trigonometric We now extend the definitions of the trigonometric functions to any size of angle, which greatly broadens the range of applications of trigonometry. Contents Subject aims and general information Important symbols and abbreviations Module 1: Equations, manipulation and word problems 1.1 Factorising the sum ofand difference between two cubes
8/11/2006 · 8.7 Right Triangle Trigonometry R1 Right Triangle Trigonometry G E T T I N G S T A R T E D 8.7 The origins of trigonometry, from the Greek trigonon (angle) and metria (mea-sure), can be traced to the ancient Egyptian, Babylonian, and Indian civilizations more than 3000 years ago. The name trigonometry, however, first appeared in 1595 as the title of the book Trigonometria published … = 90 , π 4 = 45 , πc 3 Trigonometric Ratios In a right-angled triangle, let θ be one of the remaining angles. Recall that the hypotenuse is the side not involving the right angle. Of the other two sides, one is adjacent (or touching) θ and the other is opposite. Using these, we make the following definitions: adjacent hypotenuse q opposite The sine of θ, abbreviated “sinθ”, is
About the HELM Project
Circles Pythagoras and Trigonometry Calculate. Definition 2.1: Trigonometric Functions of a General Angle Let θ be an angle in standard position and suppose that ( x , y ) is any point other than ( 0 , 0 ) on the terminal side of θ (Figure 2.3)., For angles that are obtuse (angle is greater than 90°) or negative, we use the following trigonometric ratios. The x and y variables are the values of the x and y coordinates, respectively. The r variable represents the distance from the origin, to the point (x,y). This value can ….
1 Identities Kaysons Education
Trigonometry Tutorial Nipissing University. Use the appropriate trigonometric ratio to find the value of x. Ans: 10.5 6. Use the appropriate trigonometric ratio to find the value of . Ans: 68 7. Use the appropriate trigonometric ratio to find the value of away is Ans: 46 8. The angle of elevation to the top of the empire state building from a distance 1 mile 11 . Find the height of the building to the nearest foot. Ans: .19 miles 9. In, Trigonometry+of+Right+Triangles as the one shown in Figure 5, is a triangle that has one angle measuring 90!!. The side opposite to the right angle is the longest of the three sides and it is called the hypotenuse. Since the sum of the three angles has to be 180!! (in plane geometry), the other two angles are acute angles (less than 90!!). If you label one of the acute angles ! ", then the.
incident angle at the water-air interface is now larger than the critical angle. This This phenomenon of total internal reflection is used to trap light in fibers. For angles that are obtuse (angle is greater than 90°) or negative, we use the following trigonometric ratios. The x and y variables are the values of the x and y coordinates, respectively. The r variable represents the distance from the origin, to the point (x,y). This value can …
Math 30-1: Trigonometry One PRACTICE EXAM The angle 210° is equivalent to: A. degrees C the mass is lower than 3.2 m for a duration of: 42. A Ferris wheel with a radius of 15 m rotates once every 100 seconds. Riders board the Ferris wheel using a platform 1 m above the ground. The trigonometric function that gives the height of the rider as a function of time is: A. C. D. B. 43. The Youhave probably met the trigonometric ratios cosine, sine, and tangent in a right angled triangle, and have used them to calculate the sides and angles of those triangles. In this booklet we review the definition of these trigonometric ratios and extend the concept of cosine, sine and tangent. We define the cosine, sine and tangent as functions of all real numbers. These trigonometric
Right Angle - An angle that is 90 degrees (often represented with the letter C) Acute Angle - An angle that is less than 90 degrees (often represented with letters A and B) Hypotenuse - The side of a right triangle that is across from (opposite) the right angle (often represented Adv Alg/Precal Trig Basics Notes 6 Reference Angles – the angle between the terminal side and the x-axis – are always positive and less than 90
Definition 2.1: Trigonometric Functions of a General Angle Let Оё be an angle in standard position and suppose that ( x , y ) is any point other than ( 0 , 0 ) on the terminal side of Оё (Figure 2.3). Unit Circle Trigonometry Labeling Special Angles on the Unit Circle Labeling Special Angles on the Unit Circle We are going to deal primarily with special angles around the unit circle, namely the multiples of 30o, 45o, 60o, and 90o. All angles throughout this unit will be drawn in standard position. First, we will draw a unit circle and label the angles that are multiples of 90o. These angles
demonstrate an understanding of factoring polynomials of degree greater than 2 demonstrate an understanding of angles in standard position, expressed in degrees and radians develop and apply the equation of the unit circle solve problems, using the six trigonometric ratios for angles expressed in radians and degrees graph and analyze the trigonometric functions sine, cosine, and tangent to Right Angle - An angle that is 90 degrees (often represented with the letter C) Acute Angle - An angle that is less than 90 degrees (often represented with letters A and B) Hypotenuse - The side of a right triangle that is across from (opposite) the right angle (often represented
Reference Angle: For an angle in standard position, its reference angle is the angle between 0° and 90° measured from the T‐axis (positive or negative) to its terminal side. The reference angle can be trig functions of given angles, we have been able to find the values of those functions in quadrant II. θ x y r O (x,y) θ O (-4,3) 5. Trig in Four Quadrants Page 4 To expand our knowledge, let’s look at the signs of the coordinates in the four quadrants. x values to the left of the y axis are negative; those to the right are positive. y values below the x axis are negative; those above are
trigonometric ratio of angle θ. Kaysons Education Trigonometric Functions and Identities Page 3 Let OM = x, MP = y and OP = r > 0. The circular functions are defined as: Trigonometric ratio (or functions) may also be defined with respect to a triangle. In a right angled triangle ABC, ∠CAB = A and ∠BCA = 90º = π/2. AC is the base, BC the altitude and AB is the hypotenuse. We refer to the = 90 , π 4 = 45 , πc 3 Trigonometric Ratios In a right-angled triangle, let θ be one of the remaining angles. Recall that the hypotenuse is the side not involving the right angle. Of the other two sides, one is adjacent (or touching) θ and the other is opposite. Using these, we make the following definitions: adjacent hypotenuse q opposite The sine of θ, abbreviated “sinθ”, is
Trigonometry – Cumulative Review #1 Chapter 9 : Trig Basics What you need to know!! Special Right Triangles: Use to find exact trig values of 30 , 45 , 60 . The Unit Circle: use to find trig functions of quadrantal (multiple of 90 ) angles All Student Take Calculus: Tells you which trig function is positive in which quadrant. Please note: a trig function’s RECIPROCAL function has the same Trigonometry+of+Right+Triangles as the one shown in Figure 5, is a triangle that has one angle measuring 90!!. The side opposite to the right angle is the longest of the three sides and it is called the hypotenuse. Since the sum of the three angles has to be 180!! (in plane geometry), the other two angles are acute angles (less than 90!!). If you label one of the acute angles ! ", then the
itself, all angles are necessarily less than 90 . We now extend the definitions of the trigonometric We now extend the definitions of the trigonometric functions to any size of angle, which greatly broadens the range of applications of trigonometry. For angles that are obtuse (angle is greater than 90°) or negative, we use the following trigonometric ratios. The x and y variables are the values of the x and y coordinates, respectively. The r variable represents the distance from the origin, to the point (x,y). This value can …
The Mathematics Test is a 60-question, 60-minute examination that measures mathematics reasoning abilities. The test focuses on the solution of practical quantitative problems that are to form a triangle (they form a triangle if and only if the sum of any two of them is greater than the third). But if one can form a triangle, then the angles of that triangle are indeed
Geometry Notes – Chapter 7 Right Triangles Dan Shuster
1 Identities Kaysons Education. trigonometric ratio of angle Оё. Kaysons Education Trigonometric Functions and Identities Page 3 Let OM = x, MP = y and OP = r > 0. The circular functions are defined as: Trigonometric ratio (or functions) may also be defined with respect to a triangle. In a right angled triangle ABC, в€ CAB = A and в€ BCA = 90Вє = ПЂ/2. AC is the base, BC the altitude and AB is the hypotenuse. We refer to the, The Mathematics Test is a 60-question, 60-minute examination that measures mathematics reasoning abilities. The test focuses on the solution of practical quantitative problems that are.
Trigonometric ratios schoolwires.henry.k12.ga.us. •find solutions of trigonometric equations •use trigonometric identities in the solution of trigonometric equations Contents 1. Introduction 2 2. Some special angles and their trigonometric ratios 2 3. Some simple trigonometric equations 2 4. Using identities in the solution of equations 8 5. Some examples where the interval is given in radians 10 www.mathcentre.ac.uk 1 c mathcentre 2009, incident angle at the water-air interface is now larger than the critical angle. This This phenomenon of total internal reflection is used to trap light in fibers..
Trigonometry Cumulative Review #1 Chapter 9 Trig Basics

Trigonometry Cumulative Review #1 Chapter 9 Trig Basics. = 90 , π 4 = 45 , πc 3 Trigonometric Ratios In a right-angled triangle, let θ be one of the remaining angles. Recall that the hypotenuse is the side not involving the right angle. Of the other two sides, one is adjacent (or touching) θ and the other is opposite. Using these, we make the following definitions: adjacent hypotenuse q opposite The sine of θ, abbreviated “sinθ”, is Use the appropriate trigonometric ratio to find the value of x. Ans: 10.5 6. Use the appropriate trigonometric ratio to find the value of . Ans: 68 7. Use the appropriate trigonometric ratio to find the value of away is Ans: 46 8. The angle of elevation to the top of the empire state building from a distance 1 mile 11 . Find the height of the building to the nearest foot. Ans: .19 miles 9. In.

An obtuse angle is one greater than a right angle (90°) but less than 180°. A straight angle is one whose sides form a continuous straight line (180°). A reflex angle is one greater than a straight angle (180°) but less than a circle (360°). Any two lines meeting at a point form two angles, one less than a straight angle of 180°(unless exactly a straight angle) and the other greater than = 90 , π 4 = 45 , πc 3 Trigonometric Ratios In a right-angled triangle, let θ be one of the remaining angles. Recall that the hypotenuse is the side not involving the right angle. Of the other two sides, one is adjacent (or touching) θ and the other is opposite. Using these, we make the following definitions: adjacent hypotenuse q opposite The sine of θ, abbreviated “sinθ”, is
Unit Circle Trigonometry Labeling Special Angles on the Unit Circle Labeling Special Angles on the Unit Circle We are going to deal primarily with special angles around the unit circle, namely the multiples of 30o, 45o, 60o, and 90o. All angles throughout this unit will be drawn in standard position. First, we will draw a unit circle and label the angles that are multiples of 90o. These angles The ACT Math Test assesses the mathematical skills students are expected to obtain before grade 12 (meaning through advanced algebra and basic trigonometry, but not calculus).
For angles that are obtuse (angle is greater than 90°) or negative, we use the following trigonometric ratios. The x and y variables are the values of the x and y coordinates, respectively. The r variable represents the distance from the origin, to the point (x,y). This value can … A trigonometric equation is an equation whose variable is expressed in terms of a trigonometric function value. To solve a trigonometric equation, we use the same procedures that we used to solve algebraic equations. For example, in the equation 4 sin u15 5 7, sin u is multiplied by 4 and then 5 is added. Thus, to solve for sin u, first add the opposite of 5 and then divide by 4. 4 sin u15 5 7
Youhave probably met the trigonometric ratios cosine, sine, and tangent in a right angled triangle, and have used them to calculate the sides and angles of those triangles. In this booklet we review the definition of these trigonometric ratios and extend the concept of cosine, sine and tangent. We define the cosine, sine and tangent as functions of all real numbers. These trigonometric •find solutions of trigonometric equations •use trigonometric identities in the solution of trigonometric equations Contents 1. Introduction 2 2. Some special angles and their trigonometric ratios 2 3. Some simple trigonometric equations 2 4. Using identities in the solution of equations 8 5. Some examples where the interval is given in radians 10 www.mathcentre.ac.uk 1 c mathcentre 2009
Trigonometry – Cumulative Review #1 Chapter 9 : Trig Basics What you need to know!! Special Right Triangles: Use to find exact trig values of 30 , 45 , 60 . The Unit Circle: use to find trig functions of quadrantal (multiple of 90 ) angles All Student Take Calculus: Tells you which trig function is positive in which quadrant. Please note: a trig function’s RECIPROCAL function has the same Trigonometry+of+Right+Triangles as the one shown in Figure 5, is a triangle that has one angle measuring 90!!. The side opposite to the right angle is the longest of the three sides and it is called the hypotenuse. Since the sum of the three angles has to be 180!! (in plane geometry), the other two angles are acute angles (less than 90!!). If you label one of the acute angles ! ", then the
trigonometric ratio of angle θ. Kaysons Education Trigonometric Functions and Identities Page 3 Let OM = x, MP = y and OP = r > 0. The circular functions are defined as: Trigonometric ratio (or functions) may also be defined with respect to a triangle. In a right angled triangle ABC, ∠CAB = A and ∠BCA = 90º = π/2. AC is the base, BC the altitude and AB is the hypotenuse. We refer to the Trigonometry – Cumulative Review #1 Chapter 9 : Trig Basics What you need to know!! Special Right Triangles: Use to find exact trig values of 30 , 45 , 60 . The Unit Circle: use to find trig functions of quadrantal (multiple of 90 ) angles All Student Take Calculus: Tells you which trig function is positive in which quadrant. Please note: a trig function’s RECIPROCAL function has the same
In trigonometry, angles are represented by the Greek letter theta (Оё). The sine of an angle Оё, abbreviated as sin Оё, is the ratio expressed when the side of a right triangle opposite the angle demonstrate an understanding of factoring polynomials of degree greater than 2 demonstrate an understanding of angles in standard position, expressed in degrees and radians develop and apply the equation of the unit circle solve problems, using the six trigonometric ratios for angles expressed in radians and degrees graph and analyze the trigonometric functions sine, cosine, and tangent to
A SunCam online continuing education course Basic Trigonometry, Significant Figures, and Rounding - A Quick Review (Free of Charge and Not for Credit) 8/11/2006 · 8.7 Right Triangle Trigonometry R1 Right Triangle Trigonometry G E T T I N G S T A R T E D 8.7 The origins of trigonometry, from the Greek trigonon (angle) and metria (mea-sure), can be traced to the ancient Egyptian, Babylonian, and Indian civilizations more than 3000 years ago. The name trigonometry, however, first appeared in 1595 as the title of the book Trigonometria published …
Adv Alg/Precal Trig Basics Notes 6 Reference Angles – the angle between the terminal side and the x-axis – are always positive and less than 90 •find solutions of trigonometric equations •use trigonometric identities in the solution of trigonometric equations Contents 1. Introduction 2 2. Some special angles and their trigonometric ratios 2 3. Some simple trigonometric equations 2 4. Using identities in the solution of equations 8 5. Some examples where the interval is given in radians 10 www.mathcentre.ac.uk 1 c mathcentre 2009
incident angle at the water-air interface is now larger than the critical angle. This This phenomenon of total internal reflection is used to trap light in fibers. In each case, the trigonometric ratio and its relationship to an acute angle is established in the introductory lesson and then this relationship is applied to determine the lengths of sides in a right triangle in a follow-up lesson.
Trigonometry+of+Right+Triangles as the one shown in Figure 5, is a triangle that has one angle measuring 90!!. The side opposite to the right angle is the longest of the three sides and it is called the hypotenuse. Since the sum of the three angles has to be 180!! (in plane geometry), the other two angles are acute angles (less than 90!!). If you label one of the acute angles ! ", then the Use the appropriate trigonometric ratio to find the value of x. Ans: 10.5 6. Use the appropriate trigonometric ratio to find the value of . Ans: 68 7. Use the appropriate trigonometric ratio to find the value of away is Ans: 46 8. The angle of elevation to the top of the empire state building from a distance 1 mile 11 . Find the height of the building to the nearest foot. Ans: .19 miles 9. In